2024年7月2日,由数学与统计学院负责组织的暑期国际学堂《高级拓扑优化:非线性和屈曲》线上全英文课程圆满结课。本课程由法国雷恩大学教授Balaji Raghavin教授主讲,在zoom线上会议平台授课。
本课程主要面向对拓扑优化有浓厚兴趣的研究生或本科大四学生,重点放在涉及弹性不稳定性(屈曲)和材料/几何非线性的问题上。本课程的前几讲将会对许多基础内容进行讲解,这些课程将涵盖以下基本主题:线性/非线性连续介质力学的正式介绍、材料行为的理论方面、非线性(大应变、塑性)、动态载荷、MMA 算法的使用、模型还原,以及使用 MATLAB(二维和三维)进行有限元分析和 TopOpt(拓扑优化) 的专门实践课程。

Balaji Raghavin教授非常注重力学理论基础和编程实践能力,对于弹性力学中的基础概念,如应力应变等,结合二维,三维不同情况进行讲解,并说明其中的差异与变化。随后向学生们介绍张量的基本概念和性质,连续介质热力学与本构模型、非线性弹性、三维小应变与有限应变塑性,给出了弹性力学中的重要方程的张量形式。
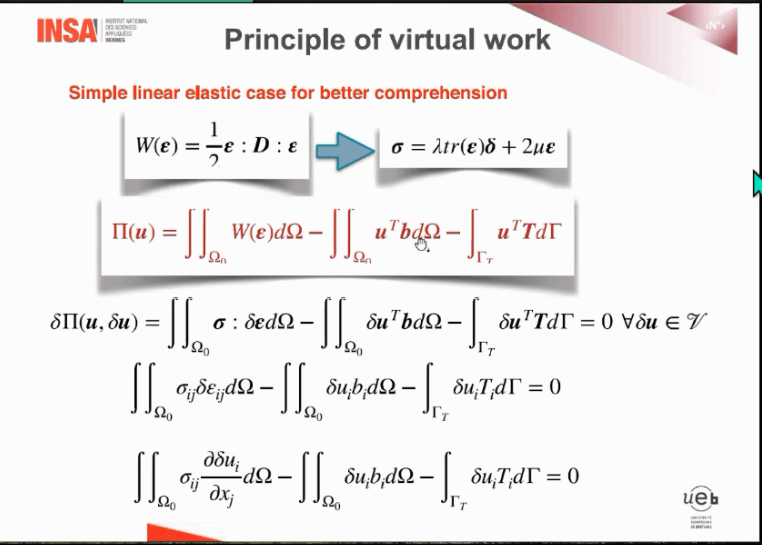
同时,由之前所给出的弹性力学公式出发,结合变分原理及求解微分方程的弱形式出发,向学生们展示了有限元方法的建立过程,并且详细介绍了有限元方法所需要用到的形函数的相关知识。
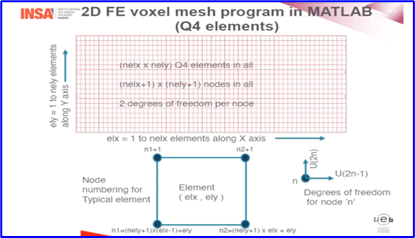
在编程实践上,Balaji Raghavin教授向学生们清楚详细的讲解了如何利用matlab建立有限元单元矩阵的方法,并结合具体的案例,对于不同的网格和载荷情况,给出不同的改进办法。
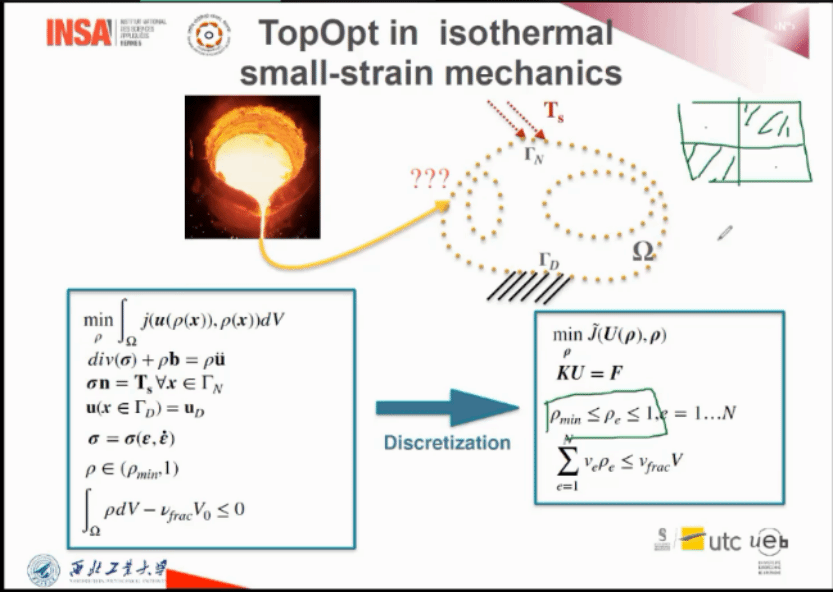
之后,Balaji Raghavin教授向学生们介绍了工程中所使用的拓扑优化的基本概念,以及在拓扑优化中所使用到的优化方法和过滤方法,并结合matlab编程实践向学生们展示(二维/三维)拓扑优化的基本流程和方法。
在之后的课程中,Balaji Raghavin教授向学生们介绍了线性屈曲的基本概念和假设以及利用有限元方法对于一维欧拉杆屈曲情况下的方程建立和求解。

在接下来的课程中,Balaji Raghavin教授在之前的基础上建立了屈曲条件下的有限元单元矩阵以及如何在屈曲条件下进行灵敏度分析。随后Balaji Raghavin教授介绍了对于线性屈曲和非线性屈曲拓扑优化领域内的一些重要文章的基本思想,鼓励学生们进行更加深入的探索。


本课程共24学时,Balaji Raghavin教授详细阐述弹性力学的力学基础知识及有限元方法,对工程领域中的拓扑优化进行了介绍,并扩展了线性屈曲情况下的拓扑优化方法,在理论课程外,利用matlab结合具体的案例实践提高了学生们的实践能力。Balaji Raghavin教授授课期间,积极和学生们问答互动,激发学生们的学习兴趣。
在课程结束时,肖曼玉老师对本次课程作了总结和回顾,她向Balaji Raghavin教授表示了由衷的感谢。本次课程得到了学生的积极反馈,也为下年度暑期课程的举办积累了宝贵的经验。
专家介绍:
Balaji Raghavan,2004年获美国宾夕法尼州立大学硕士学位,2012年获法国贡比涅技术大学博士学位,博士论文曾荣获法国计算结构力学协会(CSMA)年度最佳博士论文奖。2013年至今,法国雷恩国家科学与工程研究所土木与机械工程系终身教授。主要从事多物理场的材料性能的多尺度建模和数值模拟研究。目前与波兰的NCBC大学和法国的UTC大学以及英国伦敦玛丽女王大学都有相关的合作研究,已在该领域多个顶级期刊发表学术论文五十多篇,并担任多个知名国际期刊审稿人、编委。
文:肖曼玉 段涵予
图:段涵予
审核:都琳

 英文
英文



 微信二维码
微信二维码